
domingo, 14 de junio de 2009
EVALUACION
a) Ordenación de datos
b) Distribución de datos
c) Determina el MTC
d) Determinar el MD
60,75,82,77,65,70,67,65,78,73,69,66,72,66,68,74,61,66,74,79,67,74,80,75,70,66,76,78,79,75,72,79,69,70,74,72.
-Ordenación de datos-
60,61,65,65,66,66,66,66,67,67,68,69,69,70,70,70,72,72,72,73,74,74,74,74,75,75,75,76,77,78,78,79,79,79,80,82.
Calculemos la media, la mediana y la moda
X = ∑X/N = 2583/36
X= 71.75
Me = 72
Mo= No hay moda
Rango (82 - 60) = 22
rango = 22
S2 = ∑ (X -X)2 / N
S2 = 1068.7506 / 36
S2 = 29.6875
Desviacion típica
S = 5.4486
Coeficiente de variabilidad
CV = S/ X
CV = 5.4486 / 71.75 = 0.0759
0.0759 = 7.59 %
EJERCICIO 2
26,26,27,28,29,30,33,35,35,35,35,36,36,37,37,37,38,40,41,42,42,43,44,46,46,49,51,52,52,54,54,57,59,60,60.
X = 41.4857
Me = 40
Mo = 35
rango = (60 - 26) = 31
rango = 31
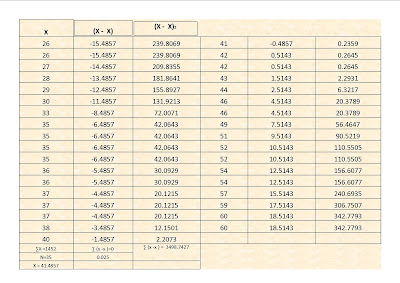
S2 = ∑(X - X) 2
S2 = 3498.7421/35
S2 = 99.9640771
Coeficiente de variabilidad Desviacion tipica
CV = S/X S = r. cuadrada 99.9640
9.9981/41.4857 S= 9.9981
CV = 0.2140 = 241 %
EJERCICIOS
43,45,47,48,49,49,49,50,50,50,50,50,51,52,52,52,52,52,52,53,53,53,54,54,54,54,55,55,56,57.
x= ∑X/N = 1544/30
X=51.46 66
Me= 78
Mo= No hay
Rango = ( 57 - 43 ) = 14 Rango = 14

S2 = ∑ ( X - X)2/N Desviacion tipica
S2= 297.4662/30 S= r. cuadrada S2 = 9.9155
S2= 9.9155 S= 3.1488
Coeficiente de variabilidad
CV= S/X
CV = 3.1488/51.4666 = 0.0611 0.0611 = 6.11 %
-EVENTOS INDEPENDIENTES Y DEPENDIENTES-
P/E, si echamos un volado dos veces, es claro, que si cae primero águila esto no afecta la probabilidad que el segundo caiga sol o nuevamente águila.
Si por lo contrario, la ocurrencia de un evento afecta la ocurrencia de eventos subsecuentes se dice que los eventos son dependientes.
Sean independientes o dependientes los eventos, se tratan de experimentos aleatorios consecuntes como una serie de intentos o repeticiones de la misma índole en los cuales se plantea la probabilidad de que se den; sucesiva o simultanea mente dos eventos .
Para eventos independientes; la regla es la siguiente,
REGLA DE MULTIPLICACIÓN
Para hallar la probabilidad de ocurrencia de un conjunto de eventos independientes se multiplican las probabilidades separados de los eventos que comprenden al conjunto.
-REGLAS BASICAS PARA COMBINAR PROBABILIDADES-
Eventos de este tipo se conocen como EVENTOS DISYUNTOS.
La probabilidad de un eneto disyunto es una probabilidad disyunta.
Por ejemplo, la probabilidad disyunta P(A1 o A2) es la probabilidad de que ocurra cualquiera de los dos eventos, A1 o A2 o ambos. Este tipo de probabilidades se puede determinar mediante la regla siguiente:
Regla General Para La Adicion De Probabilidades
La probailidad disyunta de dos eventos A1 y A2 es igual a la suma de sus probabilidades simples menos su probabilidad conjunta.
En simbolos, P (A1 o A2) = P(A1) + P(A2) - P(A1 y A2)
Esta regla es de caracter general por que se aplica a eventos mutuamente excluyentes o no ex cluyentes.
Ejemplo:
En el experimento de tirar un dado, hallemos la probabilidad de que aprezcan el 2 o el 6.
Solucion: Es evidente que el evento "salga el 2" y el evento "salga el 6" son mutuamente escluiyentes.
por lo tanto:
Pero la probabilidad de que el 2 yel 6 ocurra simultaneamente es cero.
P (2 o 6) = 1/6+1/6=0
Eventos formados por dos o mas eventos simples, se visualizan mucho mejor y se logran comprender cabalmente, mediante los diagramas de Venn, metodo diseñado en 1880 por el logico britanico Jhon Venn para la presentacion grafica de eventos u de los relaciones entre ellos.
En el contexto de la teoria de la probabilidad, un diagrama de Venn emplea lo siguiente:
1. Circulos o rectangulos para representar diversas clases de eventos.
2. Entrelazamiento de los circulos para representar la posibilidae nocurrencia de eventos conjuntos o simultaneos;
3. Areas de la grafica para rrepresentar probabilidades de ocurrencia, aunque, por lo general, aquellos no se dibujan a escala.
El espacio muestral se simboliza por una S.
Puesto que definir un espacio muestral es incluir todos los resultados posibles de un experimento, la probabilidad de que el resultado de cualquier intento dado provenga del espacio muestral es, por fuerza , igual o no.
ejemplos:


PROBABILIDAD SUBJETIVA Y PROBABILIDADES A FAVOR
En ocasiones, las probabilidades subjetivas se estiman haciendo uso del concepto de probabilidades a favor. Consiste en una forma alternativa de expresar una probabilidad sea o no subjetiva.
Si la probabilidad de ocurrencia de un evento se denoa por P y la de su no ocurrencia por
Entonces las probabilidades a favor del evento se definen como la razon de p a q. Por convenccion, estas posibilidades se expresan como la razon de 2 enteros positivos, c a d. que carecen de factores comunes.
ejemplo:
En cierta escuela universitaria, la probabilidad de que un alumno de nuevo ingreso concluya sus estudios sin deber ninguna aigantura es .38.
Solucion: sea p = .38 entonces q = 1 - p = 1 - .38 = .62
p/q = .38/.62 = 38/62 =19 (2) / 31 (2)
Por la regla convencional de que se debe siempre poner primero mayor, diremos que la probabilidades de que el alumno termine sus estudios sin deber nunguna materia estan en contra 31 a 19.
PROBABILIDAD BAJO EL ENFOQUE DE FRECUENCIA RELATIVA Y LA LEY DE LOS GRANDES NUMEROS
La probabilidad de un evento es la frecuencia observada de ese en un numero muy grande de casos.
Sean n un numero grande de intentos o repeticiones de un experimento aleatorio: f, las veces que un resultado especifico ocurre en ellos y P (A), la probabilidad de ese resultado en cada intento.
Entonces, la probabilidad f/n es la probabildad P(A).
Esto, en notación sintética, se escribe así:
P (A) es congruente f/n, cuando n es grande
El teorema de BERNOULLI, conocido también como LEY DE LOS GRANDES NÚMEROS, puede ser ilustrado repitiendo un gran numero de veces un experimento aleatorio sencillo, por ejemplo, echar volados o tirar un dado y anotar de vez en cuando, digamos cada 25 repeticiones.
La proporción en que se representa cierto resultado, tabular lo para mejor visualiacion, hacer la representacion gráfica correspondiente. De un modo semejante salio este gráfico.

Por la gran variedad de aplicaciones que tiene este teorema en la estimación de POSIBILIDADES, es necesario que nos convenzamos, por vía empírica, de la verdad que encima. Esta ley permite estibar probabilidades a proporción de veces que u hecho haya ocurrido en el pasado en un gran numero de repeticiones bajo la misma situación.
La exigencia del enfoque de frecuencia relativa: que las repeticiones, a parte de numerosas, a parte de numerosas, sean iguales en lo esencial. Que se repitan bajo las mismas condiciones.
PROBABILIDAD BAJO EL ENFOQUE CLASICO
sábado, 13 de junio de 2009
DEFINICION Y PROPIEDADES DE LA PROBABILIDAD
Es un numero que se asigna a un evento para inidicar la posibilidad de su ocurrencia.
Una probabilidad no puede ser cualquier numero, digamos -2 o 110% si no un numero real, P, que se asigna a un evento A que tiene las propiedades siguientes:
1. La probabilidad de que ocurra A no puede ser menor que cero ni mayor que uno. El cero indica la imposibilidad de ocurrencia del suceso: el uno, la certidumbre de que ocurriria.
2. Para dos eventos A1 Y A2 mutuamnete excluiyentes, la probabilidad de ocurrencia de uno u otro igual ala suma de sus propiedades separadas.
En simbolos:
P(A1 Y A2)= P(A1)+P(A2), si A1 y A2 son mutuamente excluyentes.
La expresion mutuamente excluyentes, cuyo significado explicamos quiere decir que si ocurre uno de los eventos de un espacion muestral, ninguno de los datos puede ocurrir al mismo tiempo; la ocurrencia de cualquiera de ellos excluye automaticamente la de los restantes: (la probabilidad de que sucedan A1 y A2 es cero).
P(A1 y A2)= 0 si A1 y A2 son mutuamnete excluyentes
Si A1 y A2 son mutuamente o sea que juntos abarcan todo el espacio muestra, la probabilidad de ocurrencia de uno u otro sigue siendo la suma de las probabilidades separadas, pero en este caso esa suma es igual a uno.
P(A1 o A2)= P(A1)+P(A2)= 1, si A1 y A2 son mutuamente excluyentes y exhaustivos.
ESPACIO MUESTRAL Y EVENTO
El conjunto de todos los resultados posibles de un experimento aleatorio se conoce como ESPACIO MUESTRAL, cada uno de ellos es un punto muestral y el resultado que obtenemos o esperamos obtener al realizar una o varias veces el mismo experimento es un EVENTO o SUCESO. Si el experimento se repite dos o mas veces, el numero de resultados posibles notoriamente al igual que la naturaleza de los puntos muestrales.
Ejemplo:
Determinemos el espacio muestral resultante de echar dos volados.
Solución:Se trata de un experimento formado por dos repeticiones del mismo tipo: echar un volado,pensando un poco encontraremos que los resultados posibles pueden ser dos águilas,un águila y un sol,un sol y una águila, dos soles:
{AA, AS, SA, SS}
Si el evento esperado es cualquiera de estos puntos,se dice que es un EVENTO CONJUNTO ya que consta de mas de un evento simple.
Como acabamos de ver,la determinación del espacio muestral de experimentos que implican una o dos repeticiones de su tipo,como echar uno o dos volados,tirar dos veces un dado,plantear
tener dos hijos,es muy fácil ya que basta una simple inspección.
Cuando se quiere conocer todos los resultados posibles de una serie de experimentos o repeticiones del mismo tipo, para resolver estos casos existe una técnica conocida como DIAGRAMA DE ÁRBOL cuya ampliación conduce metodicamente al espacio muestral que se quiere conocer.
TEORIA DE LA PROBABILIDAD
Si lanzamos una piedra al vacio, sabemos de ante mano que caera, podemos incluso predesir a donde, conociendo el angulo de inclinacion y la velocidad inicial del lanzamiento, si la del viento en ese momento es despresiable.
Estos experimentos, cuyos resultados pueden ser antisipados con toda certeza, reciben el nombre de fenomenos DETERMINISTAS.
Si, en cambio, tiramos un dado en cuyas caras aperescan los simbolos del 1 al 6 deconocemos cual de ellos quedara asi arriba, o si echamos un volado, ignoramos si la moneda caera aguila o sol.
Estos experimentos, en que no es posible adelantar el resultado con toda sertidumbre, se le conoce como fenomenos ALEATORIOS y son el objeto de estudio de la teoria de la probabilidad.
UNA MANERA DE INTERPRETAR EL COEFICIENTE DE VARIABILIDAD
1. Recopilado un conjunto de datos de variable cardinal, su media jamas podrá ser nula; en otras palabras ;: nunca valdrá cero. La desviacion típica, en cambio, si se puede ser nula: ello sucede cuando los datos del conjunto coinciden todos con su media.
2. Por lo tanto, dado que el coeficiente de variación se define como la relación que guarda la desviacion estándar a la media aritmética de un conjunto de datos (CV= S/X), el valor mínimo que puede adoptar un coeficiente de variación es 0, lo cual significa la inexistencia de dispersión de los datos.
De lo anterior se desprende una manera simple de interpretar coeficiente de variación: cuanto mas cercano a 0 se a su valor,mayor homogeneidad de los datos y viceverso.
COEFICIENTE DE VARIABLE
UN METODO ABREVIADO DE OBTENCION DE LA VARIANZA Y LA DESVIACION ESTANDAR
Por definicion; se sabe que:

Entonces, podemos escribir: NS= SUM(X-X)2
viernes, 12 de junio de 2009
DESVIACION ESTANDAR Y VARIANZA
en simbolos se expresa asi:
S= √∑(X-X)2 / N
Una vez hallada en uncaso concreto, debe ser expresada en las mismas unidades de la variable estudiada. Ahora vamos a aprender a calcular, explicando de paso el significado de cada una de sus terminos con forme surgan durante el procedimiento.
1. Se calcula la medida y se resta a de cada uno de los valores de las variables. Esto procede un conjunto de desviaciones con respecto a la media (x-x) que se elevan al cuadrado para detener las desviaciones cuadraticas (x-x)2. Una de las razones elevar al cuiadrado las desviacones simples es eliminar los svalores negativos, la suma de los valores (x-x) es siempre cero.
2. Se fectua la suma de las desviaciones cudraticas respecto a la media : ∑(x-x)2. Este valor se conoce brevemente como la suma de los cuuadraddo.
3. Se divide la suuma de los cuadrados entre el numero de datos de la distribuccion . El cociente representa la media de las desviaciones cuadraticas y tiene amplio uso entre el alanisis estadistico se le concoce como varianza ; S .
4. Finalmente para allar la desviacion estandar se extrae raiz cuadrada a la varianza.
